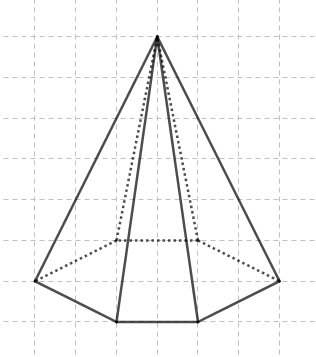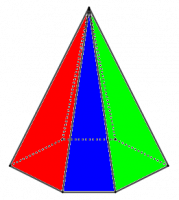
Pyramide en perspective cavalière
Méthode de la base
Pour représenter une pyramide en perspective cavalière, une méthode relativement simple est de tracer la base puis de placer le sommet de la pyramide ; ensuite on trace les arêtes latérales.
Un tétraèdre
En prenant une base triangulaire, on obtient un tétraèdre (mot qui signifie 4 faces : tétra pour quatre et èdre pour face).
On trace le triangle et on place le sommet .
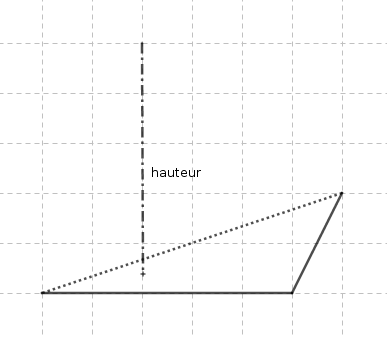
On trace les arêtes latérales, en trait plein ou en pointillé selon que les faces sont cachées ou visibles.
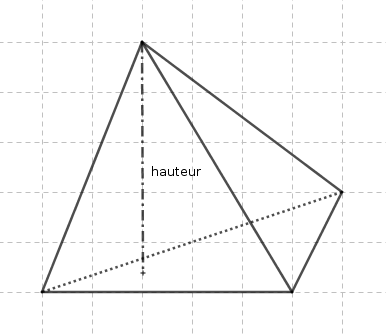
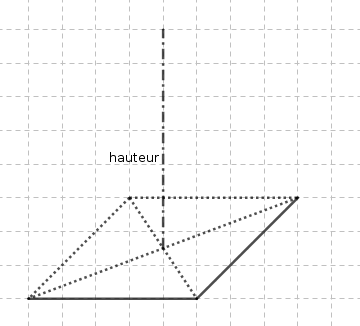
- On peut faire en sorte que la hauteur soit une arête, comme dans l’exemple suivant :
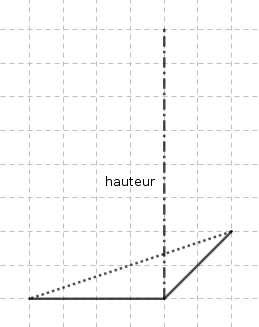
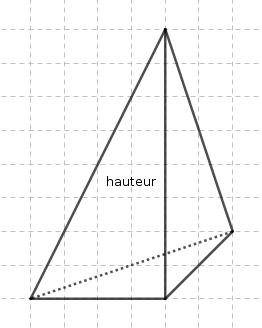
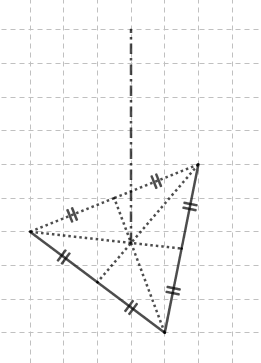
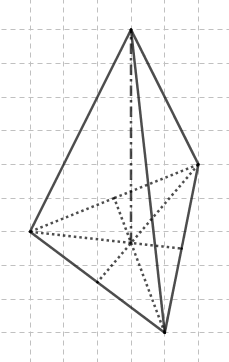
- Si la base est un triangle équilatéral, et si le pied de la hauteur est le centre du triangle équilatéral, on obtient un tétraèdre régulier, comme dans l’exemple suivant :
Une pyramide à base carrée ou rectangulaire
Dans le cas d’une base carrée, si le pied de la hauteur est le centre du carré, on obtient une pyramide régulière.
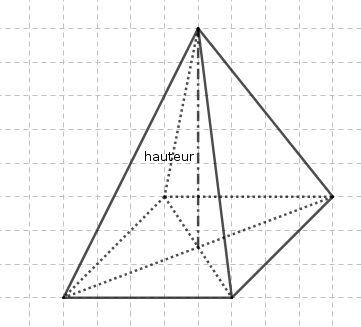
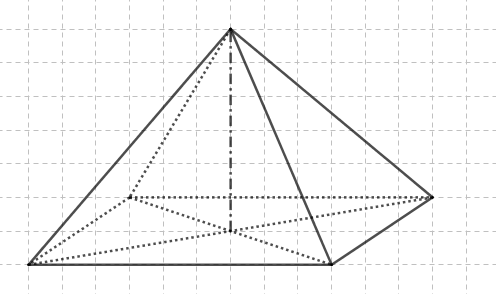
Si on prend une base rectangulaire non carrée, on n’obtient plus une pyramide régulière, même si le pied de la hauteur est le centre du rectangle :
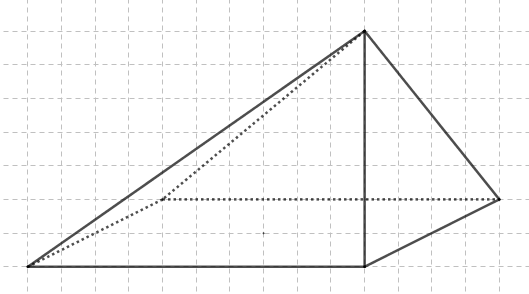
On peut aussi faire en sorte que la hauteur soit une arête :
Une pyramide à base hexagonale