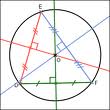
Cercle circonscrit à un triangle
A partir d’un cercle, il est facile d’inscrire un triangle : il suffit de prendre 3 points sur le cercle :-)
Inversement, il est moins simple, à partir d’un triangle, de tracer le cercle qui passe par ses 3 sommets (on dit que le cercle est circonscrit au triangle).
Cercle passant par 2 points
Puisque ce problème est moins simple, on peut se contenter, dans un premier temps, de chercher comment faire passer un cercle par 2 points.
Supposons que nous ayons réussi à construire un cercle qui passe par 2 points A et B, comme sur la figure suivante :
Nous avons nommé O le centre du cercle et tracé 2 rayons : [OA] et [OB] ; nous avons donc un triangle isocèle en O, c’est le triangle AOB. Ce qui explique qu’il y a un axe de symétrie pour cette figure ; d’ailleurs, si vous déplacez le point O, vous verrez qu’il se déplace sur une droite qui est justement l’axe de cette symétrie.
Cet axe de symétrie est d’ailleurs celui de la symétrie qui échange A et B : c’est la médiatrice du segment [AB].
Ainsi, nous pouvons constater que, d’une part, le centre d’un cercle qui passe par les points A et B est situé sur la médiatrice du segment [AB] et, d’autre part, si nous prenons un point sur la médiatrice de [AB], nous obtenons le centre d’un cercle qui passe par les points A et B.
Cela nous permet donc de tracer des cercles qui passent par 2 points A et B donnés en utilisant le programme suivant :
– tracer la médiatrice de [AB]
– prendre un point O sur la médiatrice de [AB]
– tracer le cercle de centre O et qui passe par A : il passe aussi par B
Le problème de tracer un cercle qui passe par 2 points a donc une infinité de solution… Sur la figure suivante, il est tracé plusieurs de ces cercles qui passent par A et B.
Cercle passant par 3 points
Maintenant, si nous avons 3 points A, B et C, pour qu’il soit possible d’avoir un cercle qui passe par ces 3 points, il est nécessaire qu’il passe par 2 de ces 3 points, A et B par exemple, mais aussi B et C ou C et A.
Si nous prenons les points A et B, ce que nous avons vu avec 2 points nous montre qu’il est nécessaire que le centre du cercle cherché soit sur la médiatrice de [AB].Mais si nous prenons les points B et C, le centre doit être sur la médiatrice de [BC].
Ainsi, le centre O du cercle cherché doit être à l’intersection de la médiatrice de [AB] et celle de [BC], ce qui donne OA = OB = OC et donc O est aussi sur la médiatrice de [AC].
Cela nous permet donc de tracer le cercle qui passe par les 3 points A, B et C avec le programme suivant :
– tracer la médiatrice de [AB]
– tracer la médiatrice de [BC]
– nommer O l’intersection de ces 2 droites
– tracer le cercle de centre O et qui passe par A : il passe aussi par B et par C
<geogebra|doc=967>
Nous voyons donc que, contrairement au problème avec 2 points, il n’y a qu’une seule solution au problème de tracer un cercle passant par 3 points.
Quelques animations
| Animations | Instruments utilisés |
| centre à l’intérieur du triangle | compas et règle |
| centre à l’extérieur du triangle | compas et règle |
| centre sur un des côtés | compas et règle |
Documents joints
circonscrit01bis.ggb - fichier geogebra - 3.3 ko
circonscrit02bis.ggb - fichier geogebra - 5.5 ko
circonscrit03.ggb - fichier geogebra - 6 ko
