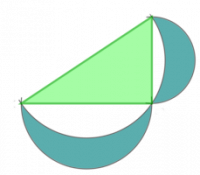
Cercle circonscrit d’un triangle rectangle
Pourquoi un triangle qui a un angle droit s’appelle-t-il un triangle rectangle ?
La réponse est très simple : car c’est la moitié d’un rectangle.
Regardez la figure ci-dessous :
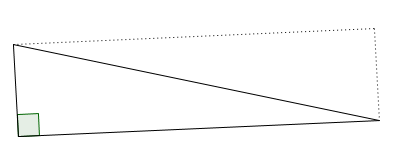
Pour tracer le cercle qui passe par les 3 sommets du triangle rectangle (on dit qu’il est circonscrit au triangle), il suffit donc de tracer le cercle qui passe par les 4 sommets du rectangle.
Mais c’est très simple : il suffit de tracer les diagonales du rectangle ; elles se coupent en un point qui est le centre du cercle.

En effet, dans un rectangle, les diagonales sont de la même longueur et se coupent en leurs milieux, ce qui veut dire que les quatre demi-diagonales sont des rayons du cercle de centre ce point d’intersection et passant par les sommets.
Cela nous montre donc que le centre du cercle circonscrit à un triangle rectangle est le milieu de son hypoténuse. Avec une figure dynamique à l’aide de geogebra :
Ce qui donne le théorème suivant :
Pour tout triangle rectangle, le cercle circonscrit a pour centre le milieu de son hypoténuse.
Documents joints
figure 3 - fichier geogebra - 3.9 ko
