Définition

Un losange est un quadrilatère dont les quatre côtés ont la même longueur.

Plus de précisions sont données dans le lexique.

Théorème

• Tout losange est un parallélogramme.

• Tout losange a ses diagonales perpendiculaires.

Démonstration

– Soit un losange. Nommons-le $ABCD$. Il s’agit de montrer que $ABCD$ est un parallélogramme.

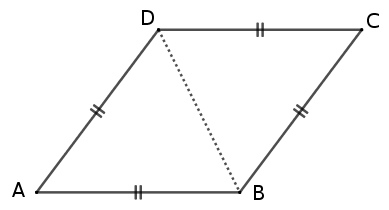
Considérons la diagonale [BD] : on a 2 triangles, ABD isocèle en A (donc $\widehat{ABD}$ = $\widehat{ADB}$) et BDC isocèle en C (donc $\widehat{CBD}$ = $\widehat{CDB}$), qui ont leurs trois côtés égaux 2 à 2, ils sont donc superposables (cas d’égalité des triangles) et,en conséquence, $\widehat{ABD}$ = $\widehat{CDB}$ = $\widehat{CBD}$ = $\widehat{BDA}$

$\widehat{ABD}$ et $\widehat{CDB}$ sont des angles alternes-internes
ils sont égaux donc $(AB)$ // $(CD)$

de même, $\widehat{ADB}$ et $\widehat{CBD}$ sont des angles alternes-internes
ils sont égaux donc $(AD)$ // $(CB)$

ainsi, $ABCD$ a ses côtés opposés parallèles : c’est donc un parallélogramme CQFD.

– Soit un losange. Nommons-le $ABCD$. Il s’agit de montrer que $ABCD$ a ses diagonales $[AC]$ et $[BD]$ perpendiculaires.

Considérons les 2 diagonales $[AC]$ et $[BD]$ du losange $ABCD$ et nommons $O$ leur point d’intersection.

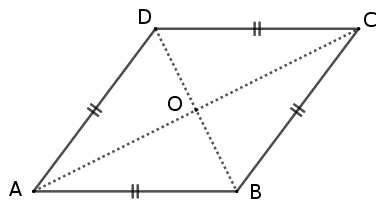
$ABCD$ est un losange donc c’est un parallélogramme : ses diagonales se coupent en leurs milieux ; par exemple, $O$ est le milieu de $[BD]$.

$ABCD$ est un losange donc, en particulier, $DCB$ est isocèle en C donc $\widehat{OBC}$ = $\widehat{ODC}$

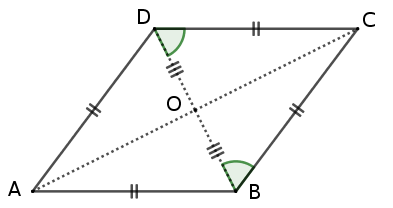
ainsi, les 2 triangles $OBC$ et $ODC$ ont 2 côtés égaux $BC$ = $DC$, $OB$ = $OD$ et 2 angles égaux $\widehat{OBC}$ = $\widehat{ODC}$ ils sont
donc superposables (cas d’égalité des triangles).

Il en résulte, notamment, que $\widehat{DOC}$ = $\widehat{BOC}$
donc $\widehat{BOD}$ est partagé en 2 angles égaux.
Or, $O \in [BD]$ donc $\widehat{BOD}$ = $180°$
donc $\widehat{DOC}$ = $\widehat{BOC}$ = $90°$
donc $(AC) \perp (BD)$
ce qui montre que les diagonales de $ABCD$ sont perpendiculaires CQFD.

Remarque : partage du losange en quatre

Au cours de la 2^e démonstration, à la place du triangle $DCB$ on aurait pu utiliser l’un des trois autres triangles $CBA$, $BAD$, $ADC$ isocèles respectivement en $B$, en $A$, en $D$.

On obtient ainsi 4 triangles rectangles en $O$ superposables : $DOC$, $COB$, $BOA$, $AOD$ qui partagent le losange $ABCD$ en 4 parts égales.

Cas particulier : les carrés

Un carré ayant ses côtés égaux est donc un losange : il en résulte qu’un carré est un parallélogramme et que ses diagonales sont perpendiculaires.