Dans quels cas un quadrilatère est-il un parallélogramme ? Les différents points du théorème suivant donnent un élément (parfois deux éléments) à vérifier avant de conclure qu’on a un parallélogramme ; on pourra ensuite utiliser les différentes propriétés des parallélogrammes.

Remarque : la définition des parallélogrammes donnent aussi des critères à vérifier [1] pour avoir un parallélogramme.

Théorème

• Si on a un quadrilatère et si ses diagonales se coupent en leurs milieux alors c’est un parallélogramme.

• Si on a un quadrilatère convexe [2] et si les côtés opposés sont égaux deux à deux alors c’est un parallélogramme.

• Si on a un quadrilatère convexe et si deux côtés opposés sont parallèles et de la même longueur alors c’est un parallélogramme.

Démonstration

– Soit un quadrilatère dont les diagonales se coupent en leurs milieux. Nommons-le $ABCD$ et soit $O$ le point d’intersection de ses deux diagonales $[AC]$ et $[BD]$ . Il s’agit de démontrer que $ABCD$ est un parallélogramme.

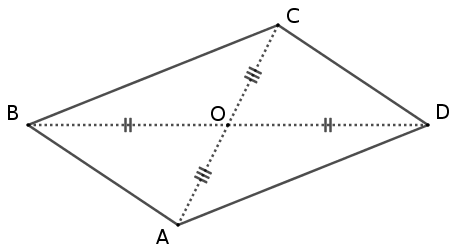
$[AC]$ et $[BD]$ se coupent en $O$ donc $\widehat{AOD}$ et $\widehat{BOC}$ sont opposés par leur sommet $O$
donc ils sont égaux : $\widehat{AOD}$ = $\widehat{BOC}$
$O$ est le milieu de $[AC]$ donc $AO$ = $OC$
$O$ est le milieu de $[BD]$ donc $BO$ = $OD$
donc les deux triangles $AOD$ et $BOC$ ont 2 angles égaux et les côtés de ces angles égaux deux à deux
donc, d’après le 1^er cas d’égalité des triangles, $AOD$ et $BOC$ sont superposables
donc $\widehat{ADB}$ = $\widehat{DBC}$
ces deux angles étant alternes-internes, il en résulte que $(AD)$ // $(CB)$

de même, en utilisant les triangles $AOB$ et $DOC$, un raisonnement semblable montre qu’ils sont superposables et donc $\widehat{CAB}$ = $\widehat{ACD}$
ces deux angles étant alternes-internes, il en résulte que $(AB)$ // $(CD)$

ainsi, le quadrilatère $ABCD$ a ses côtés opposés parallèles deux à deux, c’est donc un parallélogramme. CQFD

– Soit un quadrilatère convexe dont les côtés opposés sont égaux deux à deux. Nommons-le $ABCD$ : par hypothèse, on a $AB$ = $CD$ et $AD$ = $CB$. Il s’agit de démontrer que $ABCD$ est un parallélogramme.

Considérons, de plus, la diagonale $[AC]$ [3] : on a alors 2 triangles $ABC$ et $ADC$.

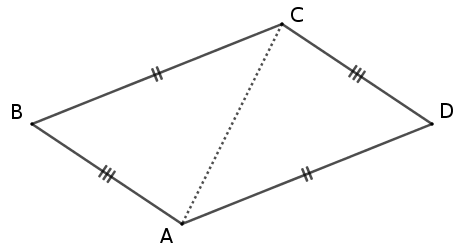
Ces deux triangles ont leurs côtés égaux deux à deux : $AB$ = $CD$, $AD$ = $CB$, leur côté commun $[AC]$ : on est donc dans le 3^e cas d’égalité des triangles ; les 2 triangles $ABC$ et $ADC$ sont superposables.

Il en résulte que, d’une part, $\widehat{BAC}$ = $\widehat{DCA}$
et comme ce sont deux angles alternes-internes, on a donc $(AB)$ // $(DC)$
et, d’autre part, $\widehat{DAC}$ = $\widehat{BCA}$
qui sont aussi deux angles alternes-internes, on a donc $(AD)$ // $(BC)$

ainsi, le quadrilatère $ABCD$ a ses côtés opposés parallèles deux à deux, c’est donc un parallélogramme. CQFD

– Soit un quadrilatère convexe dont 2 côtés opposés sont égaux et parallèles. Nommons-le $ABCD$ et supposons que les côtés opposés égaux et parallèles sont $[AB]$ et $[CD]$ : $AB$ = $CD$ et $(AB)$ // $(CD)$. Il s’agit de démontrer que $ABCD$ est un parallélogramme.

Considérons, de plus, la diagonale $[AC]$ [3] : on a alors 2 triangles $ABC$ et $ADC$.

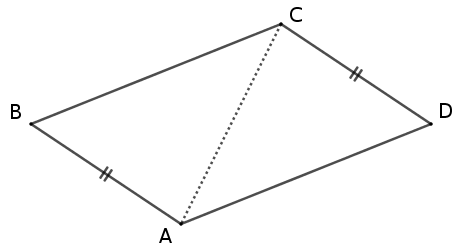
On a $(AB)$ // $(CD)$ donc les angles alternes-internes $\widehat{BAC}$ et $\widehat{DCA}$ sont égaux : $\widehat{BAC}$ = $\widehat{DCA}$.

Ainsi, les deux triangles $ABC$ et $ADC$ ont deux côtés égaux $\widehat{BAC}$ = $\widehat{DCA}$ et les côtés de ces deux angles égaux deux à deux, $AB$ = $CD$ et $[AC]$ côté commun : on est donc dans le 1^er cas d’égalité des triangles ; les 2 triangles $ABC$ et $ADC$ sont superposables.

Il en résulte que $\widehat{DAC}$ = $\widehat{BCA}$
qui sont deux angles alternes-internes, on a donc $(AD)$ // $(BC)$

ainsi, le quadrilatère $ABCD$ a ses côtés opposés parallèles deux à deux, c’est donc un parallélogramme. CQFD