Théorème

Si deux droites et une sécante déterminent des angles alternes-internes égaux alors ces deux droites sont parallèles.
 
Réciproquement, si deux droites sont parallèles et si une sécante détermine des angles alternes-internes avec ces deux droites alors ces angles alternes-internes sont égaux.

Remarque : on a le même théorème en remplaçant alternes-internes par correspondants.

Démonstration

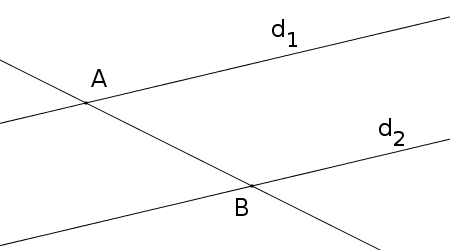
– Considérons 2 droites $d_1$ et $d_2$ et une droite sécante qui coupe $d_1$ en $A$ et $d_2$ en $B$ et supposons que 2 angles alternes-internes sont égaux :

Soit $M$ le milieu de $[AB]$ et traçons la droite qui est perpendiculaire à la droite $d_1$ et qui passe par $M$ : elle coupe $d_1$ en $C$ et $d_2$ en $D$.

Les angles $\widehat{CMA}$ et $\widehat{DMB}$ sont opposés par le sommet M : ils sont donc égaux.

Ainsi, les triangles $ACM$ et $BDM$ sont tels que $AM=MB$, $\widehat{CAM} = \widehat{MBD}$ et $\widehat{CMA} = \widehat{DMB}$
donc, d’après le 2^e cas d’égalité, ils sont superposables
donc $\widehat{BDM} = \widehat{ACM}$.

Or, $\widehat{ACM}$ est un angle droit donc $\widehat{BDM}$ aussi
donc les droites $(CD)$ et $d_2$ sont perpendiculaires
donc $d_1$ et $d_2$ sont perpendiculaires à $(CD)$

donc $d_1$ et $d_2$ sont parallèles. CQFD

– Considérons 2 droites $d_1$ et $d_2$ et une droite sécante qui coupe $d_1$ en $A$ et $d_2$ en $B$ et supposons que les droites $d_1$ et $d_2$ sont parallèles :

Traçons la droite qui est perpendiculaire à la droite $d_1$ et qui passe par $A$ : elle coupe $d_2$ en $C$
De même, traçons la droite qui est perpendiculaire à la droite $d_2$ et qui passe par $B$ : elle coupe $d_1$ en $D$

Les droites $d_1$ et $d_2$ sont parallèles et la droite $(AC)$ est perpendiculaire à $d_1$
donc $(AC)$ est perpendiculaire à $d_2$ aussi.
De même, $(BD)$ est perpendiculaire à $d_1$

Ainsi, le quadrilatère $ACBD$ a 4 angles droits, c’est donc un rectangle et donc ses côtés opposés sont égaux : $AD = BC$ et $DB = CA$

Considérons les triangles $ADB$ et $BCA$ : ils sont tels que $\widehat{ADB} = \widehat{BCA}$, $DA = CB$ et $DB = CA$
donc, d’après le 1^er cas d’égalité, ils sont superposables
donc $\widehat{DAB} = \widehat{CBA}$

ce qui montre que les angles alternes-internes sont égaux. CQFD

– Si on a des angles correspondants, on peut facilement obtenir des angles alternes-internes et inversement. Pour le comprendre, regardons la figure suivante.

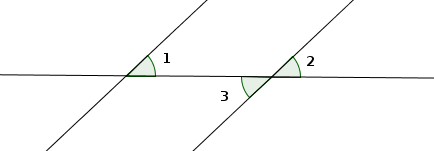
Les angles 1 et 2 sont correspondants et les angles 1 et 3 sont alternes-internes.

Or les angles 2 et 3 sont opposés par le sommet donc ils sont égaux.

En conséquence, si on a des angles correspondants 1 et 2 égaux, il en résulte qu’on a des angles alternes-internes 1 et 3 égaux ; et inversement. D’où la remarque.