Définition

Un rectangle est un quadrilatère dont les quatre angles sont des angles droits.

Plus de précisions sont données dans le lexique.

Théorème

• Tout rectangle est un parallélogramme

• Tout rectangle a ses diagonales de la même longueur

Démonstration

– Soit un rectangle, nommons-le $ABCD$. Il s’agit de montrer que $ABCD$ est un parallélogramme.

$ABCD$ est un rectangle donc il a 4 angles droits : $\widehat{ABC} = \widehat{BCD} = \widehat{CDA} = \widehat{DAB} = 90° $
On a donc $(AB) \perp (BC)$ et $(DC) \perp (BC)$
donc $(AB)$ // $(DC)$
De même, on a $(AD) \perp (AB)$ et $(BC) \perp (AB)$
donc $(AD)$ // $(BC)$
Ainsi, $ABCD$ a ses côtés opposés parallèles donc $ABCD$ est un parallélogramme CQFD.

– Soit un rectangle, nommons-le $ABCD$. Il s’agit de montrer que ses diagonales $[AC]$ et $[BD]$ ont la même longueur.

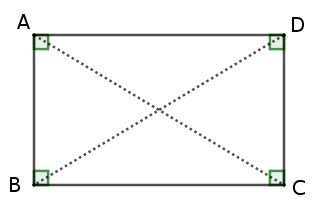
Considérons les 2 triangles $ABC$ et $ABD$.
Ils ont un côté commun $[AB]$, deux autres côtés égaux $AD$ = $BC$ [1] et 2 angles égaux $\widehat{ABC} = \widehat{DAB}$ [2]
donc ces 2 triangles sont superposables (cas d’égalité des triangles).

Il en résulte, notamment, que $AC$ = $BD$, ce qui montre que les 2 diagonales $[AC]$ et $[BD]$ ont la même longueur CQFD.

Cercle circonscrit au rectangle

$ABCD$ étant un rectangle, c’est un parallélogramme et donc les diagonales $[AC]$ et $[BD]$ se coupent en leurs milieux, nommons $O$ ce milieu commun aux deux diagonales.

Or, les diagonales d’un rectangle sont de la même longueur donc, on a $OA$ = $OB$ = $OC$ = $OD$

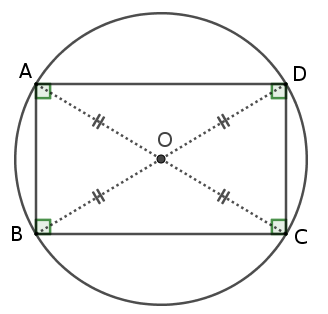
ce qui montre que le cercle de centre $O$ et qui passe par $A$ passe aussi par $B$, par $C$ et par $D$ : ce cercle est circonscrit au rectangle.

Cas particulier : les carrés

Un carré est un rectangle car un carré a quatre angles droits : il en résulte qu’un carré est un parallélogramme et que ses diagonales ont la même longueur.

De plus, un carré est inscrit dans un cercle dont le centre est l’intersection de ses diagonales.