Théorème

Pour tout triangle, les médianes d’un triangle se coupent en un même point.
De plus, ce point d’intersection est situé aux deux-tiers de chaque médiane en partant du sommet.
Ce point est le centre de gravité du triangle.

Démonstration

Considérons un triangle $ABC$, $I$ le milieu de $[AB]$, $J$ celui de $[BC]$ et $K$ celui de $[CA]$.
Soit $O$ le point d’intersection de deux médianes du triangle $ABC$, par exemple les médianes $(AJ)$ et $(BK)$. Et pour ces deux médianes, soit D le milieu de $[OB]$ et E le milieu de $[OA]$.

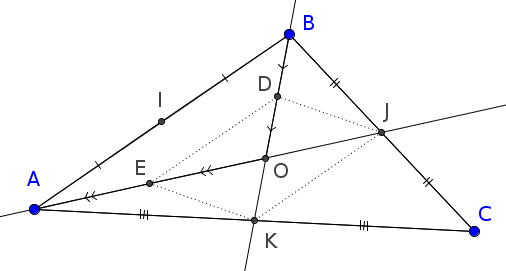
Dans le triangle $ABC$, la droite $(JK)$, passant par $J$ le milieu de $[BC]$ et $K$ celui de $[CA]$, est parallèle à la droite $(AB)$ [1].

De même, dans le triangle $ABO$, la droite $(DE)$, passant par $D$ le milieu de $[BO]$ et $E$ celui de $[OA]$, est parallèle à la droite $(AB)$.

Ainsi, $(JK)$ et $(DE)$ sont parallèles car elles sont parallèles à la même droite $(AB)$.

Considérons maintenant les triangles $AOC$ et $BOC$.

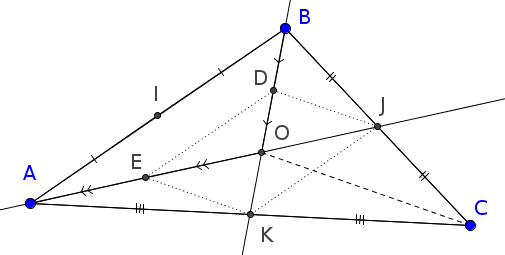
Dans ce triangle $AOC$, $E$ est le milieu de $[AO]$ et K celui de $[AC]$ donc $(EK)$ est parallèle à $(OC)$.

Et dans le triangle $BOC$, $J$ est le milieu de $[BC]$ et $D$ celui de $[BO]$ donc $(DJ)$ est parallèle à $(OC)$.

Ainsi, $(DJ)$ et $(KE)$ sont parallèles car elles sont parallèles à la même droite $(OC)$.

Il en résulte que le quadrilatère $DJKE$ a ses côtés parallèles deux à deux
donc $DJKE$ est un parallélogramme
et donc ses diagonales $[DK]$ et $[JE]$ se coupent en leur milieu.

Or $O$ est l’intersection des deux diagonales de $DJKE$ donc $O$ est le milieu de $[DK]$ et de $[JE]$.

Il en résulte que $BD=DO=OK$ et que $AE=EO=OJ$
et donc le point d’intersection de 2 médianes du triangle $ABC$ est situé aux deux-tiers de ces médianes en partant des sommets du triangle.

Il en est donc de même de la 3ème médiane qui coupent donc les deux autres en $O$.
Ainsi, les trois médianes du triangle $ABC$ se coupent en un même point. CQFD