Théorème

Tout point situé sur la bissectrice d’un angle est à égale distance de chaque côté de cet angle.
Réciproquement, tout point situé à égale distance des deux côtés d’un angle est sur la bissectrice de cet angle.

Démonstration

– Soit un angle de sommet $A$ et un point $M$ appartenant à la bissectrice de cet angle.
Considérons $HM$ et $KM$ les distances respectives de $M$ à chaque côté de cet angle : les angles $\widehat{AHM}$ et $\widehat{AKM}$ sont donc des angles droits d’après la définition de la distance d’un point à une droite.

On sait que la somme des angles d’un triangle est égale à $180°$.
Ainsi, dans le triangle $AHM$, on a : $\widehat{AMH}$=$180°-(\widehat{MAH}+\widehat{AHM})$
De même, dans le triangle $AMH$, on a : $\widehat{AMK}$=$180°-(\widehat{MAK}+\widehat{AKM})$.
Or, $\widehat{AHM}$=$\widehat{AKM}$ puisque ce sont 2 angles droits
et $\widehat{MAH}$=$\widehat{MAK}$ puisque $M$ est sur la bissectrice de $\widehat{HAK}$
On a donc $180°-(\widehat{MAH}+\widehat{AHM})=180°-(\widehat{MAK}+\widehat{AKM})$
donc $\widehat{AMH}=\widehat{AMK}$
Ce qui montre que les triangles $AMH$ et $AMK$ ont les mêmes angles.
Or, ces deux triangles ont un côté commun $[AM]$ : ils sont donc supperposables et donc leurs côtés sont égaux et donc $HM=MK$.
Ce qui montre que $M$ est à la même distance des deux côtés de l’angle considéré. CQFD

– Pour démontrer la réciproque de la propriété, considérons un angle de sommet $A$ et un point $M$ situé à la même distance de ses deux côtés.
En reprenant les mêmes notations que ci-dessus, on a $HM=MK$ et $\widehat{AHM}=\widehat{AKM}=90°$.

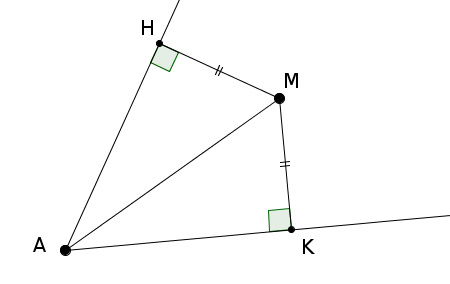
$AMH$ est un triangle rectangle en $H$ : on peut donc utiliser le théorème de Pythagore pour calculer $AH$ en fonction de $AM$ et $HM$ :
$AH^2=AM^2-HM^2$
De même, puisque $AMK$ est rectangle en $K$, on a :
$AK^2=AM^2-KM^2$
Or, $HM=MK$ donc $AM^2-HM^2=AM^2-KM^2$
donc $AH^2=AK^2$ ce qui donne $AH=AK$
Ainsi, les deux triangles $AMH$ et $AMK$ ont les mêmes côtés : ils sont donc superposables et donc ils ont les mêmes angles.
Ce qui montre que $\widehat{MAH}=\widehat{MAK}$
donc $(AM)$ est la bissectrice de l’angle $\widehat{HAK}$
donc $M$ est sur la bissectrice de l’angle considéré. CQFD