Dans quels cas un parallélogramme est-il particulier ? Les différents points du théorème suivant répondent à cette question : selon la condition supplémentaire, on peut avoir un rectangle ou un losange ; et même un carré si on a la fois un rectangle et un losange.

Théorème

• Si on a un parallélogramme et si un de ses angles est un angle droit alors c’est un rectangle.

• Si on a un parallélogramme et si deux côtés consécutifs [1] sont de la même longueur alors c’est un losange.

• Si on a un parallélogramme et si ses deux diagonales sont de la même longueur alors c’est un rectangle.

• Si on a un parallélogramme et si ses deux diagonales sont perpendiculaires alors c’est un losange.

Démonstration

– Soit un parallélogramme dont un des angles est un angle droit. Nommons-le $ABCD$ et supposons que l’angle droit est en $A$ : $\widehat{BAD}$ = 90°. Il s’agit de démontrer que $ABCD$ est un rectangle.

$ABCD$ est un parallélogramme donc $(BC)$ // $(AD)$
Or, $\widehat{BAD}$ = 90° donc $(AB) \perp (AD)$
donc $(AB) \perp (BC)$
donc $\widehat{ABC}$ = 90°

de même, $(AB)$ // $(DC)$ et $(AB) \perp (AD)$
donc $(DC) \perp (AD)$
donc $\widehat{ADC}$ = 90°

enfin, on a aussi $\widehat{BCD}$ = 90° car $\widehat{BCD}$ et $\widehat{BAD}$ sont deux angles opposés du parallélogramme $ABCD$ et que dans un parallélogramme 2 angles opposés sont égaux.

En résumé, les 4 angles de $ABCD$ sont des angles droits donc c’est un rectangle. CQFD

– Soit un parallélogramme dont deux côtés consécutifs ont la même longueur. Nommons-le $ABCD$ et supposons que les deux côtés consécutifs $[AB]$ et $[BC]$ ont la même longueur : $AB$ = $BC$. Il s’agit de démontrer que $ABCD$ est un losange.

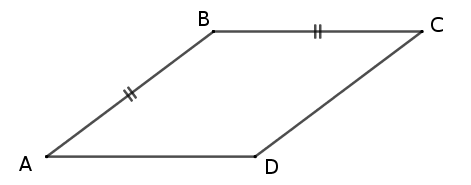
$ABCD$ est un parallélogramme donc ses côtés opposés sont égaux deux à deux : $AB$ = $CD$ et $AD$ = $BC$
Or, $AB$ = $BC$
donc $AB$ = $CD$ = $AD$ = $BC$

ainsi, $ABCD$ a ses 4 côtés égaux donc c’est un losange. CQFD

– Soit un parallélogramme dont les deux diagonales ont la même longueur. Nommons-le $ABCD$ ; les deux diagonales ont la même longueur : $AC$ = $BD$. Il s’agit de démontrer que $ABCD$ est un rectangle.

$ABCD$ est un parallélogramme donc ses deux diagonales $[AC]$ et $[BD]$ se coupent en leurs milieux ; nommons $O$ ce milieu commun aux deux diagonales.

De plus, par hypothèse, $AC$ = $BD$ donc $AO$ = $BO$ = $CO$ = $DO$ car $O$ est le milieu de $[AC]$ et aussi de$[BD]$ : on a donc 4 triangles isocèles en $O$, $AOB$, $BOC$, $COD$ et $DOA$.

On sait que, dans un triangle isocèle, les angles opposés aux côtés égaux sont égaux ; d’où la figure codée suivante (saurez-vous expliquer, par exemple, pourquoi les angles $\widehat{CBD}$ et $\widehat{ADB}$ sont égaux ? ) :

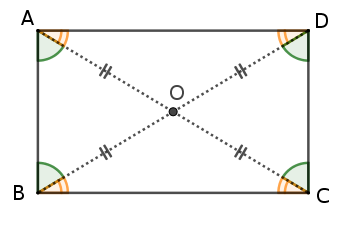
Il en résulte que $\widehat{CAB} + \widehat{ACB}$ = $\widehat{ABC}$
donc, en ajoutant $\widehat{ABC}$ aux deux côtés de l’égalité, on a :
$\widehat{ABC} + \widehat{CAB} + \widehat{ACB}$ = $2 \times \widehat{ABC}$
Or, dans un triangle, la somme des trois angles est égale à 180°, notamment dans le triangle $ABC$ : $\widehat{ABC} + \widehat{CAB} + \widehat{ACB}$ = 180°
donc $2 \times \widehat{ABC}$ = 180°
donc $\widehat{ABC}$ = 90°

ainsi, le parallélogramme $ABCD$ a un angle qui est droit donc c’est un rectangle CQFD

– Soit un parallélogramme dont les deux diagonales sont perpendiculaires. Nommons-le $ABCD$ ; les deux diagonales sont perpendiculaires : $(AC) \perp (BD)$. Il s’agit de démontrer que $ABCD$ est un losange.

$ABCD$ est un parallélogramme donc ses deux diagonales $[AC]$ et $[BD]$ se coupent en leurs milieux ; nommons $O$ ce milieu commun aux deux diagonales.

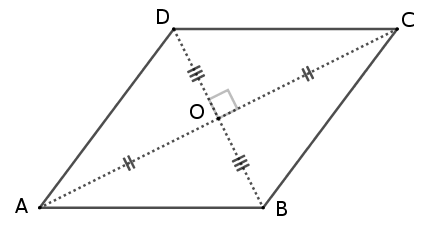
En utilisant le 1^er cas d’égalité des triangles, il en résulte que les 4 triangles $BOC$, $COD$, $DOA$ et $AOB$, tous rectangles en $O$, sont superposables.
Par exemple, $BOC$ et $COD$ ont deux angles égaux, $\widehat{BOC}$ = $\widehat{COD}$, et les côtés de ces deux angles égaux deux à deux, $BO$ = $DO$ avec $[CO]$ côté commun, donc $BOC$ et $COD$ sont superposables.
On a donc $AB$ = $BC$ = $CD$ = $DA$.

Ainsi, $ABCD$ a ses 4 côtés de la même longueur, c’est donc un losange. CQFD