Définition

Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.

Théorème

Pour tout parallélogramme, les côtés opposés ont la même longueur.

Pour tout parallélogramme, les angles opposés ont la même ouverture.

Pour tout parallélogramme, les diagonales se coupent en leur milieu.

Démonstration

– Soit $ABCD$ un parallélogramme, traçons une de ses diagonales : $[BD]$ par exemple, comme le montre la figure suivante :

$ABCD$ un parallélogramme donc les droites $(AD)$ et $(BC)$ sont parallèles donc les angles alternes-internes $\widehat{ADB}$ et $\widehat{DBC}$ sont égaux.
De même, les droites $(AB)$ et $(CD)$ sont parallèles donc les angles alternes-internes $\widehat{BDC}$ et $\widehat{DBA}$ sont égaux.

Ainsi, les triangles $ADB$ et $CDB$ ont un côté commun $[DB]$ et les angles adjacents à ce côté qui sont égaux deux à deux : ces deux triangles sont donc superposables de sorte qu’il en résulte que $\widehat{DAB}=\widehat{DCB}$, $DC=BA$ et $DA=BC$.
On a aussi : $\widehat{ADC}=\widehat{ADB}+\widehat{BDC}=\widehat{DBC}+\widehat{DBA}=\widehat{ABC}$

En résumé : les angles opposés du parallélogramme $ABCD$ sont égaux et les côtés opposés du parallélogramme $ABCD$ sont égaux. CQFD

– Reprenons la figure ci-dessus et complétons-là par la diagonale $[AC]$ : les deux diagonales se coupent en un point $O$.

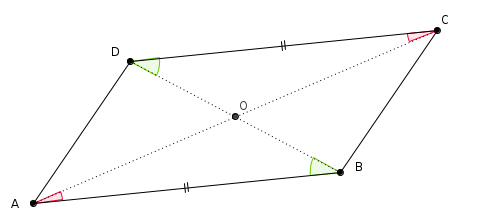
Comme ci-dessus avec les angles alternes-internes $\widehat{ADB}$ et $\widehat{DBC}$ qui sont égaux, les angles alternes-internes $\widehat{DCA}$ et $\widehat{CAB}$ sont égaux puisque les droites $(AB)$ et $(CD)$ sont parallèles.
Or $O$ est sur $[AC]$ donc $\widehat{DCA}=\widehat{DCO}$ et $\widehat{CAB}=\widehat{OAB}$
de même $O$ est sur $[DB]$ donc $\widehat{CDB}=\widehat{CDO}$ et $\widehat{ABD}=\widehat{ABO}$

On a donc $DC=BA$, $\widehat{DCO}=\widehat{OAB}$ et $\widehat{ODC}=\widehat{OBA}$ [1]
donc les triangles $ABO$ et $CDO$ sont superposables
donc $OB=OD$ et $OC=OA$

Et comme, d’une part $O$, $B$ et $D$ sont alignés, et que, d’autre part $O$, $C$ et $A$ sont alignés, cela montre que $O$ est le milieu de $[DB]$ et aussi le milieu de $[AC]$ : il en résulte que les diagonales du parallélogramme $ABCD$ se coupent en leur milieu. CQFD