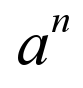
Les puissances d’un nombre
Exposant entier positif
Lorsqu’on multiplie un nombre par lui-même un certain nombre de fois, on obtient une puissance de ce nombre.
Par exemple, 
à—à—à—à—à—à— est une puissance de .
On la note 
car il y a 
facteurs égaux à .
En effectuant le calcul, on obtient : =
.
Remarque : comme est en exposant, on dit « exposant  ».
Parfois, on dit aussi « puissance  »
Les puissances de 2
De même, on obtient :
=
, 
=
, 
=
, 
=
, 
=
, 
=
, 
=
, 
=
, …
Par exemple, si on veut calculer 
, il suffit de multiplier par , ce qui donne : =
.
De même, 
=à—=à—=
.
Les puissances de sont très utilisées en informatique. Par exemple pour les capacités des supports comme les clés USB : 128 Mo, 512 Mo, 256 Mo, 1
024 Mo ( ou 1 Go), …
Les puissances de 3
=, 
=
, 
=
, 
=
, 
=
, 
=
, =, 
=
, 
=
=
Les puissances de 4
=, 
=, 
=, 
=, 
=, 
=
, 
=
, 
=
, 
=
, 
=
Les puissances de 5
=
, 
=
, 
=
, 
=
, 
=
, 
=
, 
=
, 
=
, 
=
, 
=
Exposant entier négatif
En examinant les puissances successives obtenues, on remarque que pour passer d’une puissance d’un nombre à la suivante, il suffit de multiplier par le nombre et donc, pour passer à la précédente, il suffit de diviser par le nombre.
Cela nous permet d’étendre les tables de puissances aux exposants négatifs :
…Nous connaissons , qui est égal à , donc pour obtenir 
, il suffit de diviser par : à·=
donc =.
Maintenant, nous connaissons , qui vaut , donc en le divisant par , on va obtenir :
=à·=à·=
Continuons : nous connaissons , en le divisant par 4, on obtient .
=à·=à·=à—=
=
De même :
=à·=à·=à—=
=
=à·=à·=à—=
=
=à·=à·=à—=
=
Vous avez sans doute remarqué qu’à chaque fois on obtient l’inverse de la puissance avec l’exposant positif : est l’inverse de , est l’inverse de , est l’inverse de , …
En continuant ainsi, et pour d’autres tables de puissances, nous voyons que cela est général. Par exemple, 
est l’inverse de 
.
D’où la définition suivante : 
est l’inverse de 
et la formule correspondante est : =
Remarque : il est nécessaire que 
soit différent de zéro, pour pouvoir diviser par .
Exposant égal à 0
Lorsqu’on a complété la table des puissances de pour les exposants négatifs, on a vu que = puisque cela provient de = que l’on divise par .
Pour les autres tables de puissances, par exemple celle de , on a le même résultat :
=
à·=à·=
On a donc la formule : 
= avec différent de zéro bien entendu.
Formulaire
En résumé, on a les formules suivantes :
– pour tout entier positiftel que
et pour tout nombre
– pouret pour tout nombre
– pouret pour tout nombre
,
– pour tout entier relatif
Les puissances de 10
Les puissances de 10 sont très utilisées en sciences. En voici quelques-unes.
– vers l’infiniment grand :
, 
, 
, 
, 
, 
, 
, …
↠vous avez remarqué ce nom rigolo ;-)
– vers l’infiniment petit :
, 
, 
, 
, 
, 
, …
RSS 2.0