Croisé et non-croisé ?

Dans des exercices, on mentionne souvent que le quadrilatère à considérer est non-croisé ; mais alors, que signifie croisé pour un quadrilatère ?

Pour comprendre cela, on va prendre 4 points qui seront les 4 sommets du quadrilatère. D’ailleurs, un quadrilatère [1] a 4 côtés car il a 4 sommets !

1^re disposition de 4 points

Prenons 4 points — nommés $A$, $B$, $C$ et $D$ — disposés comme ceci :

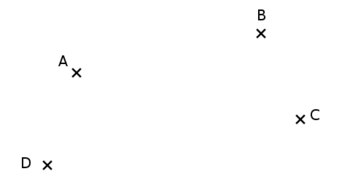
Si on nous parle du quadrilatère $ABCD$, on aura ceci :

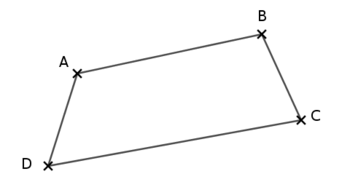
Dans ce cas, on a 4 côtés [2] : $[AB]$, $[BC]$, $[CD]$ et $[DA]$ et 2 diagonales [3] $[AC]$ et $[BD]$.

Par contre, toujours avec les 4 points $A$, $B$, $C$ et $D$ ci-dessus, si on nous parle du quadrilatère $ABDC$ (notez bien l’ordre des points), on aura ceci :

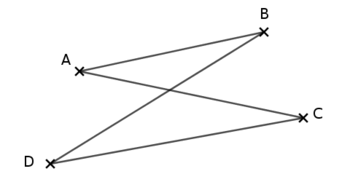
Dans ce cas, on a toujours 4 côtés : $[AB]$, $[BD]$, $[DC]$ et $[CA]$ et 2 diagonales $[AD]$ et $[BC]$.

Vous voyez donc que selon comment sont reliés 4 points, le quadrilatère obtenu n’a pas la même forme ! Ci-dessus, dans le 1^er cas il est non croisé et, dans le 2^e cas, il est croisé car les côtés $[BD]$ et $[CA]$ se croisent.

Nous avons parlé des diagonales : traçons-les en pointillés. On obtient dans chacun des cas ci-dessus ceci :

   

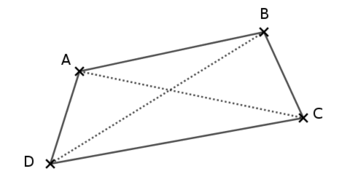
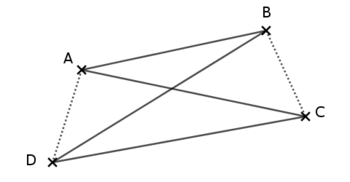
Dans le 1^er cas, les diagonales sont à l’intérieur du quadrilatère ; dans le 2^e cas, elles sont à l’extérieur du quadrilatère.

Ce que nous avons constaté avec ces 4 points disposés comme ci-dessus est-il valable pour n’importe quelle disposition de ces 4 points ?

Avant de lire la suite, essayez de répondre à la question en disposant les 4 points de plusieurs façons…

2^e disposition de 4 points

Prenons 4 points disposés comme ceci :

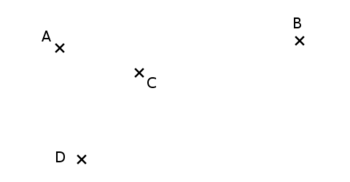
On obtient alors $ABCD$ et $ABDC$ comme ceci :

   

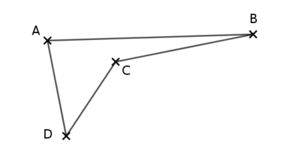
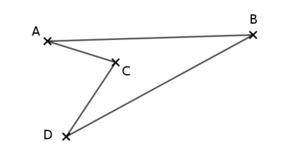
On voit donc qu’il n’est pas possible d’obtenir un quadrilatère croisé avec les 4 points de cette 2^e disposition !

Regardez les diagonales :

   

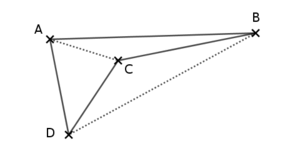
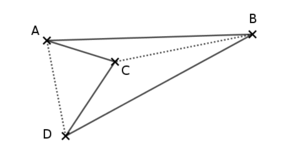
Il y en a toujours une qui est à l’extérieur du quadrilatère et l’autre à l’intérieur du quadrilatère.

Dans ce cas, on dit que le quadrilatère est concave.

3 sortes de quadrilatère

En résumé, on a 3 sortes de quadrilatère :

• croisé : les 2 diagonales sont à l’extérieur

  

• convexe : les 2 diagonales sont à l’intérieur

  

• concave : une diagonale est à l’intérieur, l’autre est à l’extérieur

  

Ainsi, si un quadrilatère n’est pas croisé, il peut être convexe ou concave.

Cas des quadrilatères particuliers

Une famille de quadrilatères particuliers est celle des parallélogrammes et, dans ce cas, ils sont tous convexes et donc non-croisés.

En effet, les diagonales d’un parallélogrammes se coupent en leur milieu et donc sont toutes les deux à l’intérieur du parallélogramme donc un parallélogramme est convexe.

Parmi les parallélogrammes, il y a les rectangles, les losanges et ceux qui sont à la fois des rectangles et des losanges et que l’on nomme des carrés.