Les cas d’égalité de deux triangles sont des théorèmes célèbres : il est très simple de les comprendre et ils rendent de grands services pour expliquer et comprendre d’autres propriétés, comme cela est fait sur ce site.

Théorème

– 1^er cas d’égalité :
Soit deux triangles $ABC$ et $DEF$ tels que $AB=DE$, $BC=EF$ et $\widehat{ABC}=\widehat{DEF}$ alors ces deux triangles sont superposables.

– 2^e cas d’égalité :
Soit deux triangles $ABC$ et $DEF$ tels que $AB=DE$, $\widehat{ABC}=\widehat{DEF}$ et $\widehat{BAC}=\widehat{EDF}$ alors ces deux triangles sont superposables.

– 3^e cas d’égalité :
Soit deux triangles $ABC$ et $DEF$ tels que $AB=DE$, $BC=EF$ et $AC=DF$ alors ces deux triangles sont superposables.

Démonstration

– 1^er cas d’égalité :
Considérons 2 triangles $ABC$ et $DEF$ tels que $AB=DE$, $BC=EF$ et $\widehat{ABC}=\widehat{DEF}$ :

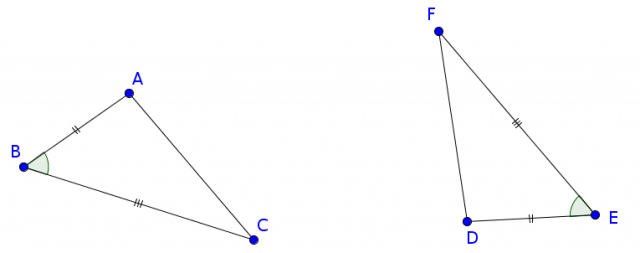
Puisque $\widehat{ABC}=\widehat{DEF}$, ces 2 angles sont superposables : on peut donc amener le sommet $B$ sur le sommet $E$, le côté $[BA)$ sur le côté $[ED)$ et le côté $[BC)$ sur le côté $[EF)$, éventuellement en effectuant un retournement.

Or, on a $AB=DE$ donc $A$ et $D$ sont superposés lorsqu’on superpose les deux angles $\widehat{ABC}=\widehat{DEF}$ comme ci-dessus,
et on a $BC=EF$ donc $C$ et $F$ sont superposés aussi dans ce même mouvement.

Ainsi, $ABC$ et $DEF$ sont superposables. CQFD

– 2^e cas d’égalité :
Considérons deux triangles $ABC$ et $DEF$ tels que $AB=DE$, $\widehat{ABC}=\widehat{DEF}$ et $\widehat{BAC}=\widehat{EDF}$ :

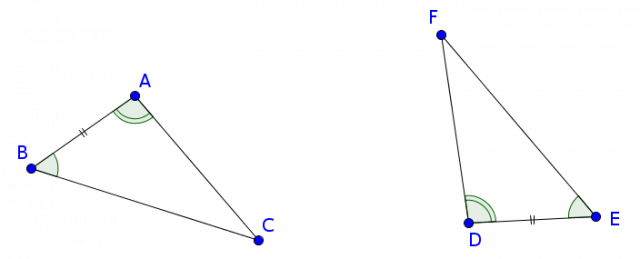
Puisque $AB=DE$, on peut superposer les deux segments $[AB]$ et $[DE]$, $A$ sur $D$ et $B$ sur $E$.

On a aussi $\widehat{ABC}=\widehat{DEF}$ donc en superposant les côtés $[BA)$ et $[ED)$ en même temps que les segments $[AB]$ et $[ED]$ (ce qui peut donner lieu à un éventuel retournement), les côtés $[BC)$ et $[EF)$ sont aussi superposés.

De même, puisque $\widehat{BAC}=\widehat{EDF}$, les côtés $[AB)$ et $[DE)$ étant superposés, les côtés $[AC)$ et $[DF)$ sont aussi superposés.

Or les demi-droites $[BC)$ et $[AC)$ se coupent en C donc l’intersection F des demi-droites $[DF)$ et $[EF)$ va se superposer sur le point C.

Ainsi, $ABC$ et $DEF$ sont superposables. CQFD

– 3^e cas d’égalité :
Considérons deux triangles $ABC$ et $DEF$ tels que $AB=DE$, $BC=EF$ et $AC=DF$ :

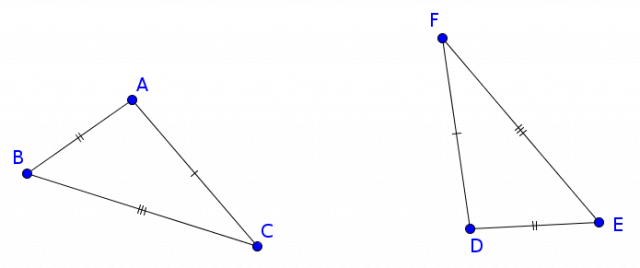
Puisque $AB=DE$, déplaçons, éventuellement en s’aidant d’un retournement, le triangle $DEF$ de sorte que $[AB]$ et $[DE]$ se superposent et que les sommets $C$ et $F$ soient de part et d’autre de $[AB]$ et traçons le segment $[CF]$ :

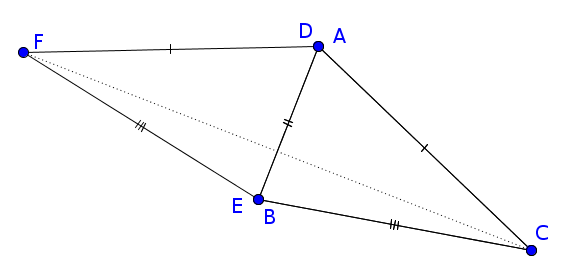
$BC=EF$ donc le triangle $BCF$ est isocèle en $B$ donc $\widehat{BCF}=\widehat{BFC}$
$AC=DF$ donc le triangle $ACF$ est isocèle en $A$ donc $\widehat{ACF}=\widehat{AFC}$
Il en résulte que l’angle $\widehat{BCA}$, somme des angles $\widehat{BCF}$ et $\widehat{FCA}$, est égal à l’angle $\widehat{BFA}$, somme des angles $\widehat{BFC}$ et $\widehat{CFA}$ [1] .
Ainsi, les triangles $ABC$ et $DEF$ sont tels que $BC=EF$, $AC=DF$ et $\widehat{BCA}=\widehat{EFD}$.
Ce qui correspond au 1^er cas d’égalité donc les triangles $ABC$ et $DEF$ sont superposables. CQFD