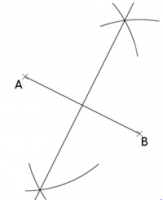
La médiatrice d’un segment
Définition
La médiatrice d’un segment est la droite qui passe par le milieu de ce segment et qui est perpendiculaire à ce segment.
Théorème
Pour tout segment, tout point de la médiatrice du segment est à égale distance des extrémités de ce segment.
Inversement, si un point est à égale distance des extrémités d’un segment, alors ce point est sur la médiatrice du segment.
Démonstration
– Soit un segment $[AB]$ et $d$ sa médiatrice.
Considérons un point $P$ sur la droite $d$ et nommons $M$ le milieu de $[AB]$ comme le montre la figure suivante :

$M$ étant le milieu de $[AB]$, on a $AM=MB$
Les points $P$ et $M$ étant sur la médiatrice de $[AB]$,
la droite $(PM)$ est perpendiculaire à $[AB]$
donc les angles $\widehat{PMA}$ et $\widehat{PMB}$ sont des angles droits
on a donc $\widehat{PMA}=\widehat{PMB}$.
Ainsi, les deux triangles $PMA$ et $PMB$ sont superposables
il en résulte que $PA=PB$. CQFD
– Inversement, soit un segment $[AB]$ et un point $P$ tel que $PA=PB$. Considérons le milieu $M$ de $[AB]$, comme sur la figure suivante :

Comme $PA=PB$, le triangle $PAB$ est isocèle en $P$
donc $\widehat{PBM}=\widehat{PAM}$
et par ailleurs, $M$ est le milieu de $[AB]$
donc $AM=MB$
ainsi, les triangles $PAM$ et $PBM$ sont superposables
donc $\widehat{PMB}=\widehat{PMA}$
Or, $M$ est sur $[AB]$ donc $\widehat{AMB}=180$°
Avec $\widehat{PMB}=\widehat{PMA}$
il en résulte que $\widehat{PMB}=\widehat{PMA}=90$°
donc $P$ est sur la médiatrice de $[AB]$. CQFD
