La réciproque du théorème de Thalès
Théorème
Si on a l’alignement des points $A$, $M$ et $B$, ainsi que l’alignement des points $A$, $N$ et $C$ de sorte que les points sont alignés dans le même ordre
et si de plus $\dfrac{AM}{AB} = \dfrac{AN}{AC}$
alors les droites $(MN)$ et $(BC)$ sont parallèles.
Ordre des points
Une précision en ce qui concerne l’ordre des points : on peut dénombrer 3 situations.
En effet, $A$ et $B$ étant donné, le point $M$ peut être situé entre $A$ et $B$ ou bien ne pas être situé entre $A$ et $B$.
Dans ce dernier cas, il y a 2 possibilités : $M$ est sur la demi-droite d’origine $A$ qui ne contient pas $B$ ou bien $M$ est sur la demi-droite d’origine $B$ qui ne contient pas $A$.
Voici 3 figures résumant ces 3 situations pour des points $A$, $M$ et $B$ alignés :



3 situations possibles
Il en résulte que si l’on veut le même ordre pour les points $A$, $N$ et $B$, on aura les 3 situations suivantes :
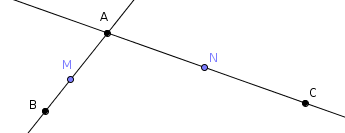
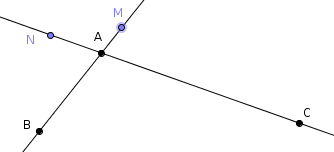
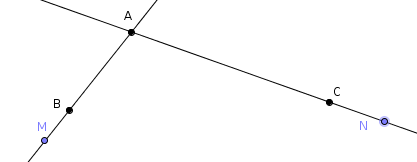
Démonstration
Plaçons-nous dans les conditions prévus par le théorème :
$A$, $M$ et $B$ alignés, $A$, $N$ et $C$ alignés dans le même ordre et $\dfrac{AM}{AB} = \dfrac{AN}{AC}$.
Prenons la 1re situation et considérons la figure suivante :
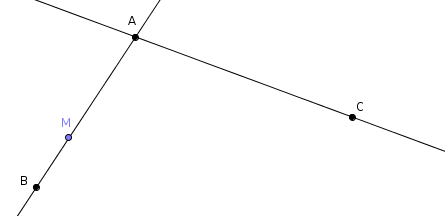
Dans cette figure, on n’a pas placé le point $N$ mais on sait qu’il est entre $A$ et $C$ puisque $M$ est entre $A$ et $B$ et que l’on a le même ordre de placement des points sur ces deux alignements. Nous y reviendrons lorsque nous aurons besoin de cette condition dans la démonstration.
On sait aussi que $\dfrac{AM}{AB} = \dfrac{AN}{AC}$.
Considérons maintenant la droite qui est parallèle à $(BC)$ et qui passe par $M$ : elle coupe $(AC)$ en un point $N’$ qui est entre $A$ et $C$.
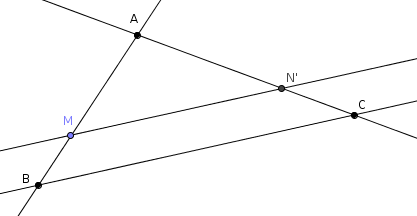
Ainsi, $A$, $M$ et $B$ sont alignés, $A$, $N$ et $C$ sont alignés et $(MN’)$ // $(BC)$
donc d’après le théorème de Thalès, $\dfrac{AM}{AB} = \dfrac{AN’}{AC}$
Or, $\dfrac{AM}{AB} = \dfrac{AN}{AC}$ donc $\dfrac{AN}{AC} = \dfrac{AN’}{AC}$
et donc $AN’ = AN$
Comme les points $A$, $N$ et $N’$ sont alignés, cette égalité ne peut se produire que dans 2 cas :
$N’ = N$ ou bien $A$ est le milieu de $[NN’]$
Le 2e cas ne peut se produire puisque $N$ et $N’$ sont tous les deux entre $A$ et $C$
On a donc le 1er cas : $N = N’$
ce qui signifie que $(MN)$ et $(MN’)$ désigne la même droite
donc $(MN)$ est parallèle à $(BC)$. CQFD
On a le même raisonnement dans les deux autres situations, comme le lecteur pourra s’en rendre compte.
