Thalès : un des premiers mathématiciens dont on se souvienne… On raconte qu’il réussit à calculer la hauteur de la plus haute pyramide d’Égypte en utilisant l’ombre qu’elle fait : savez-vous comment ?

Le théorème qui porte le nom de ce mathématicien de l’antiquité concerne des triangles semblables comme nous allons le voir ci-dessous.

 

Agrandissement et réduction

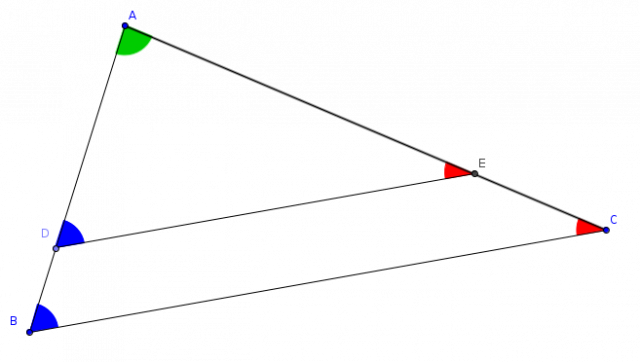
Observez la figure suivante :

Dans cette figure, on a deux triangles emboîtés $ABC$ et $ADE$, et le côté $[DE]$ est parallèle au côté $[BC]$.

Comme $[DE]$ et $[BC]$ sont parallèles, on obtient des angles correspondants égaux.

Ainsi, $ \widehat{ADE} $ = $ \widehat{ABC} $, et encore $ \widehat{AED} $ = $ \widehat{ACB} $. Bien sûr, on a $ \widehat{DAE} $ = $ \widehat{BAC} $.

Ce qui montre que les triangles $ABC$ et $ADE$ ont des angles égaux 2 à 2 : on dit que ces triangles sont semblables ; la figure ci-dessous montre les angles égaux.

Intuitivement, cela nous montre que le triangle $ABC$ est un agrandissement du triangle $ADE$ (on peut dire aussi que $ADE$ est une réduction de $ABC$).

Ainsi, les triangles $ABC$ et $ADE$ ont leurs côtés proportionnels, ce que l’on peut traduire par le tableau de proportionnalité suivant :

triangle $ADE$	$AD$	$AE$	$DE$
triangle $ABC$	$AB$	$AC$	$BC$

À la place d’un tableau de proportionnalité, on peut écrire les égalités suivantes : $\displaystyle\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}$

 

ce qui nous donne le théorème de Thalès.

Le théorème de Thalès

Si dans un triangle $ABC$, un point $D$ est sur le côté $[AB]$ et un point $E$ sur le côté $[AC]$ avec $(DE)$//$(BC)$
alors $\displaystyle\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}$

 

Un cas particulier

Un cas particulier du théorème de Thalès est obtenu en prenant $D$ au milieu de $[AB]$ :

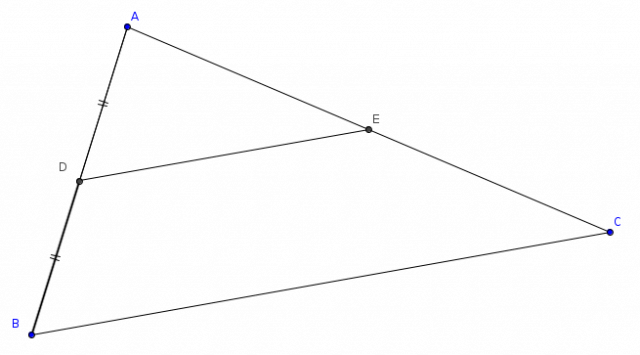
on a donc $AB = 2 \times AD$. D’après le théorème de Thalès, il en résulte les mêmes proportions pour les 2 autres côtés : $AC = 2 \times AE$ et $BC = 2 \times DE$.

On a donc $E$ qui est le milieu de $[AC]$ et $DE$ qui est la moitié de $BC$.

 

D’où le théorème suivant :

Si dans un triangle, une droite passe par le milieu d’un côté tout en étant parallèle à un autre côté alors cette droite passe par le milieu du troisième côté.

 

La droite des milieux

En considérant la figure ci-dessus, nous savons par ailleurs qu’il n’y a qu’une seule droite parallèle à $(BC)$ et qui passe par $D$ (cette propriété est connue sous le nom de l’axiome d’Euclide) donc la droite qui passe par les milieux de deux côtés d’un triangle ne peut qu’être parallèle au troisième côté.

 

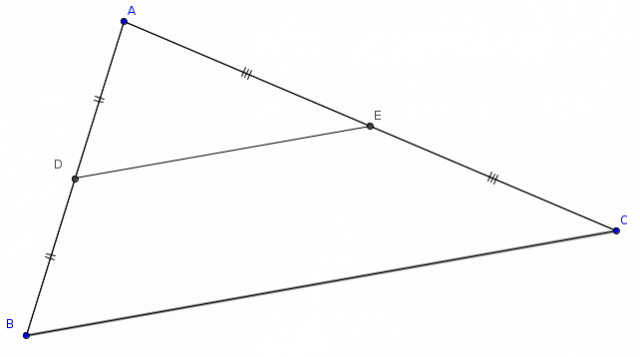
D’où le théorème de la droite des milieux :

Dans un triangle, si une droite passe par les milieux de deux côtés alors cette droite est parallèle au troisième côté.

 

Une démonstration d’Euclide

Ci-dessus, nous avons évoqué notre intuition pour expliquer que le triangle $ABC$ est un agrandissement du triangle $ADE$. Voici une explication plus rigoureuse dûe à Euclide, un autre mathématicien de l’antiquité.

Si nous traçons les segments $[DC]$ et $[EB]$, nous avons deux triangles $DBC$ et $EBC$ :

Ces deux triangles $DBC$ et $EBC$ ont leurs hauteurs, issues de $D$ et de $E$ respectivement, égales (car les droites $(DE)$ et $(BC)$ sont parallèles) associée à leur base commune $[BC]$

donc $\mathscr{A}(DBC) = \mathscr{A}(EBC)$
où $\mathscr{A}(…)$ désigne l’aire de …

en prenant les compléments des triangles $DBC$ et $EBC$ à l’intérieur du trapèze $DECB$, on a encore deux triangles $DEC$ et $DEB$ de même aire :

$\mathscr{A}(DEC) = \mathscr{A}(DEB)$

donc, en ajoutant le triangle $ADE$ aux deux triangles $DEC$ et $DEB$, on a encore des triangles de même aire : $\mathscr{A}(ADC) = \mathscr{A}(AEB)$

Maintenant, traçons la hauteur $[DH]$ issue de $D$ pour le triangle $ACD$ et la hauteur $[EK]$ issue de $E$ pour le triangle $AEB$.

L’égalité $\mathscr{A}(ADC) = \mathscr{A}(AEB)$ donne alors

$$\frac{AC \times DH}{2} = \frac{AB \times EK}{2}$$

d’où $AC \times DH = AB \times EK$

Par ailleurs, $\mathscr{A}(ADE)$ peut être exprimée en fonction de la hauteur $KE$ ou de la hauteur $DH$. On obtient

$$\frac{AD \times EK}{2} = \frac{AE \times DH}{2}$$

donc $AD \times EK = AE \times DH$

En divisant les deux égalités obtenues, on a :

$$\frac{AE \times DH}{AC \times DH} = \frac{AD \times EK}{AB \times EK}$$

et en simplifiant, cela donne

$$\frac{AD}{AB} = \frac{AE}{AC}$$

Plaçons le point $F$ de $[BC]$ de sorte que $[EF]$ soit parallèle à $[AB]$ : $DEFB$ est un parallélogramme donc $DE = BF$.

Par ailleurs, dans le triangle $ABC$, $E$ est sur le côté $[CA]$, $F$ sur le côté $[BC]$ et, par construction, $(EF)$ // $(AB)$ donc on peut réutiliser le même raisonnement que ci-dessus pour obtenir :

$$\frac{EC}{AC} = \frac{CF}{CB}$$

Or, $E \in [AC]$ et $F \in [BC]$
donc $EC = AC-AE$ et $CF = BC-BF$

il en résulte que $\displaystyle\frac{AC-AE}{AC} = \frac{BC-BF}{CB}$ c’est-à -dire $\displaystyle\frac{AC}{AC} - \frac{AE}{AC} = \frac{BC}{BC} - \frac{BF}{BC}$
Or, quand on divise un nombre par lui-même, on obtient 1 : $\displaystyle\frac{BC}{BC} = \frac{AC}{AC} = 1$ donc $\displaystyle 1-\frac{AE}{AC}=1-\frac{BF}{BC}$
et donc $\displaystyle\frac{AE}{AC} = \frac{BF}{BC}$ et comme $DE = BF$, on obtient :

$$\frac{AE}{AC} = \frac{DE}{BC}$$

On a donc bien les égalités $\displaystyle\frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC}$
CQFD

 

Un réseau de parallèles

En fait, le théorème de Thalés peut être associé à une propriété des réseaux de droites parallèles, comme nous allons le voir maintenant.

Considérons un triangle $ABC$ et un partage en parts égales du côté $[AB]$ ; pour fixer les idées, supposons que ce côté $[AB]$ soit partagé en 7 parts égales.

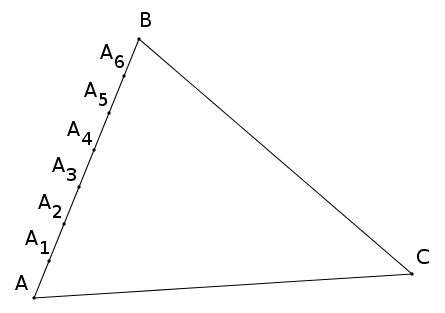
Et traçons les droites parallèles au côté $[AC]$ passant par les points correspondants au partage du côté $[AB]$.

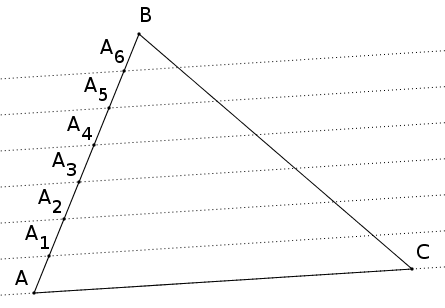
Ce réseau de droites parallèles coupent le côté $[BC]$ en 6 points comme sur la figure suivante :

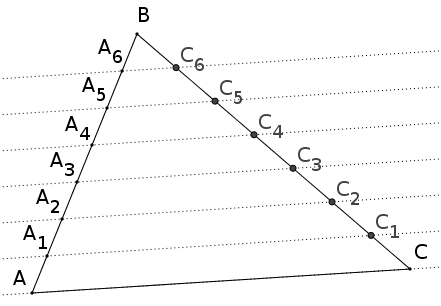
Nous allons montrer que l’on obtient un partage en parts égales du côté $[BC]$.

Pour cela, traçons la droite qui est parallèle à $(BA)$ et qui passe par $C_5$ : elle coupe la droite $(A_4C_4)$ en $D_4$ comme sur la figure suivante :

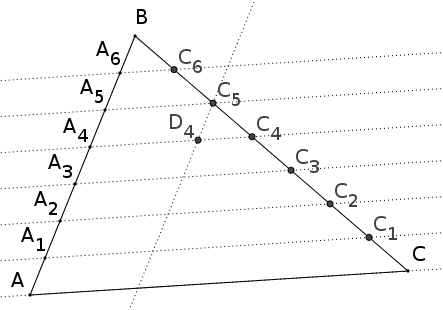
Nous allons comparer les triangles $A_6BC_6$ et $D_4C_5C_4$.

Par construction, les droites $(A_5A_4)$ et $(C_5D_4)$ sont parallèles et il en est de même des droites $(A_5C_5)$ et $(A_4D_4)$.

Il en résulte que le quadrilatère $A_5C_5D_4A_4$ est un parallélogramme
donc $A_5A_4=C_5D_4$.

Or, le partage du côté $[AB]$ étant en parts égales, $A_5A_4=A_6B$
donc $A_6B=C_5D_4$
Par ailleurs, d’une part, les droites $(BA_6)$ et $(C_5D_4)$ étant parallèles, les angles correspondants $\widehat{A_6BC_6}$ et $\widehat{D_4C_5C_4}$ sont égaux, et d’autre part, les droites $(C_6A_6)$ et $(C_4A_4)$ étant parallèles, les angles correspondants $\widehat{BC_6A_6}$ et $\widehat{C_5C_4D_4}$ sont égaux.

On sait que la somme des angles dans un triangle est égale à 180°
donc, dans le triangle $A_6BC_6$, $\widehat{BA_6C_6}=180°-(\widehat{A_6BC_6}+\widehat{BC_6A_6})$
et comme $\widehat{A_6BC_6}=\widehat{D_4C_5C_4}$ et $\widehat{BC_6A_6}=\widehat{C_5C_4D_4}$, il en résulte :
$\widehat{BA_6C_6}=180°-(\widehat{D_4C_5C_4}+\widehat{C_5C_4D_4})$
Or, dans le triangle $D_4C_5C_4$, $\widehat{C_5D_4C_4}=180°-(\widehat{D_4C_5C_4}+\widehat{C_5C_4D_4})$
donc $\widehat{BA_6C_6}=\widehat{C_5D_4C_4}$

Ainsi, les triangles $A_6BC_6$ et $D_4C_5C_4$ ont leurs côtés $[A_6B]$ et $[C_5D_4]$ égaux et les angles adjacents à ces côtés égaux deux à deux : $\widehat{A_6BC_6}=\widehat{D_4C_5C_4}$ et $\widehat{BA_6C_6}=\widehat{C_5D_4C_4}$

Cela correspond à un des cas d’égalité des triangles : les deux triangles $A_6BC_6$ et $D_4C_5C_4$ sont superposables et donc $BC_6=C_5C_4$.

En reproduisant le même raisonnement à partir des points $C_6$, $C_4$, $C_3$, $C_2$ et $C_1$, on montre que les longueurs $C_6C_5$, $C_5C_4$, $C_4C_3$, $C_3C_2$, $C_2C_1$ et $C_1C$ sont toutes égales à la longueur $BC_6$ : elles sont donc toutes égales, ce qui montre que l’on a bien un partage en parts égales du segment $[BC]$ CQFD.

Prenons maintenant le point $A_3$ par exemple.
On a $A_3B=4à—A_6B$ et $AB=7à—A_6B$ donc $\displaystyle\frac{A_3B}{AB}=\frac{4à—A_6B}{7à—A_6B}=\frac{4}{7}$
de même, $C_3B=4à—C_6B$ et $CB=7à—C_6B$ donc $\displaystyle\frac{C_3B}{CB}=\frac{4à—C_6B}{7à—C_6B}=\frac{4}{7}$
il en résulte que $\displaystyle\frac{A_3B}{AB}=\frac{C_3B}{CB}$