Théorème

Pour tout triangle, la somme des trois angles est un angle plat.

Démonstration

Soit un triangle $ABC$ et reportons l’angle $\widehat{BAC}$ dans le prolongement de $[AC)$ pour obtenir l’angle $\widehat{B’CC’}$ de sorte que $C$ est le milieu de $[AC’]$, $B’$ et $B$ sont du même côté par rapport à $(AC)$, $B’C=BA$ et $\widehat{B’CC’}=\widehat{BAC}$ comme cela est indiqué sur la figure suivante :

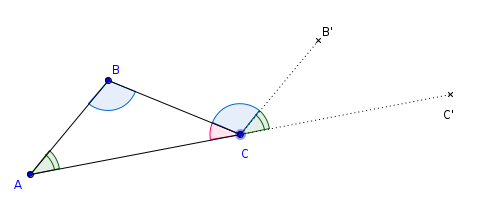
Les angles correspondants $\widehat{B’CC’}$ et $\widehat{BAC}$ étant égaux,
il en résulte que les droites $(AB)$ et $(CB’)$ sont parallèles.


Par ailleurs, les angles $\widehat{ABC}$ et $\widehat{BCB’}$ sont alternes-internes
et, comme $(AB)//(CB’)$, on a donc $\widehat{ABC}=\widehat{BCB’}$

Enfin, $\widehat{ACC’}=\widehat{ACB}+\widehat{BCB’}+\widehat{B’CC’}$ avec $\widehat{BCB’}=\widehat{ABC}$ et $\widehat{B’CC’}=\widehat{BAC}$
donc $\widehat{ACC’}=\widehat{ACB}+\widehat{ABC}+\widehat{BAC}$

Or, $C$ est sur $[AC’]$ donc $\widehat{ACC’}=180$°
donc $\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180$°

Ainsi, la somme des trois angles du triangle $ABC$ est égale à 180°. CQFD