Théorème

Pour tout triangle, les bissectrices des angles se coupent en un même point : ce point est le centre du cercle inscrit au triangle.

Démonstration

Soit $ABC$ un triangle, Considérons $d_1$ la bissectrice de $\widehat{ABC}$, $d_2$ la bissectrice de $\widehat{BCA}$ et $O$ leur point d’intersection.

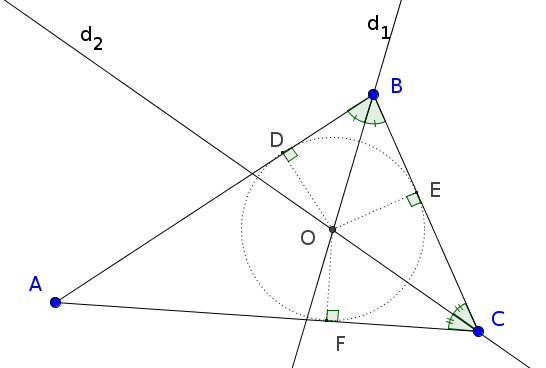
$O$ étant sur la bissectrice de l’angle $\widehat{ABC}$, $O$ est à la même distance des côtés $[BA)$ et $[BC)$ :
$OD=OE$, $(OD)\perp(AB)$ et $(OE)\perp(BC)$.

$O$ étant sur la bissectrice de l’angle $\widehat{BCA}$, $O$ est à la même distance des côtés $[CB)$ et $[CA)$ :
$OE=OF$, $(OE)\perp(CB)$ et $(OF)\perp(CA)$.

Il en résulte que $OD=OE=OF$
donc $O$ est le centre du cercle passant par $E$, $D$ et $F$

et comme $(OD)\perp(AB)$, $(OE)\perp(BC)$ et $(OF)\perp(CA)$

ce cercle est tangent aux trois côtés du triangle $ABC$ : c’est le cercle inscrit dans le triangle $ABC$.

Par ailleurs, on a aussi $OD=OF$ avec $(OD)\perp(AB)$ et $(OF)\perp(AC)$
donc $O$ est à la même distance des côtés de l’angle $\widehat{BAC}$

donc $O$ est sur la bissectrice de l’angle $\widehat{BAC}$.

En résumé, les 3 bissectrices du triangle $ABC$ se coupent en un même point qui est le centre du cercle inscrit au triangle $ABC$. CQFD