Théorème

Pour tout triangle, les médiatrices des côtés se coupent en un même point : ce point est le centre du cercle circonscrit au triangle.

Démonstration

Soit $ABC$ un triangle, $d_1$ la médiatrice de $[AB]$ et $d_2$ celle de $[BC]$
Soit $O$ le point d’intersection de $d_1$ et $d_2$ [1]

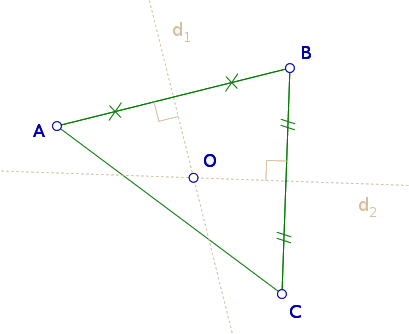
$O$ est sur $d_1$ donc $OA = OB$ [2]
$O$ est sur $d_2$ donc $OB = OC$ [2]

il en résulte que $OA = OB = OC$
ce qui montre que $A$, $B$ et $C$ sont sur un même cercle de centre $O$.

Par ailleurs, comme $OA = OC$, $O$ est sur la médiatrice de $[AC]$ [3]

Ainsi, les médiatrices des côtés du triangle $ABC$ se coupent en un même point qui est le centre du cercle circonscrit au triangle $ABC$. CQFD

Construction

Un article détaille la construction du cercle circonscrit à un triangle et donne des animations dans trois cas possibles.