Vous savez que la symétrie centrale est un demi-tour et il est donc facile de se convaincre que les propriétés suivantes sont vraies :

• Le symétrique d’un segment est un segment et ces deux segments ont la même longueur.
   
• Le symétrique d’un angle est un angle et ces deux angles ont la même ouverture.

Ce sont des propriétés qui sont aussi vraies dans le cas d’une symétrie axiale.

Cependant, dans le cas de la symétrie centrale, on a aussi la propriété suivante :

Dans une symétrie centrale, un segment et son symétrique sont parallèles.

Ce qui n’est pas toujours vrai pour la symétrie axiale.

Comment expliquer le parallélisme de 2 segments symétriques par rapport à un point ?

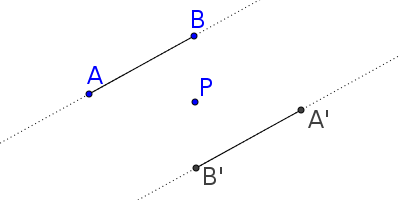
Une première idée est d’utiliser un logiciel de géométrie comme Geogebra (gratuit et d’utilisation simple) pour observer ce qu’il se passe. Ci-dessous, vous pourrez télécharger et utiliser une figure dynamique comprenant un segment [AB], un point P et le segment [A’B’] symétrique de [AB] par rapport au point P. Nous avons fait apparaître en pointillés les droites (AB) et (A’B’).

Déplacez les points P, A ou B pour vous convaincre que les 2 segments symétriques sont toujours parallèles.

Toujours ? Il y a quand même un cas, vous l’avez sans doute remarqué, très particulier : A, B et P alignés ! En fait, cela signifie que le point P est sur la droite (AB) : la droite (AB) a donc fait un demi-tour sur elle même et elle est donc son propre symétrique dans ce cas.

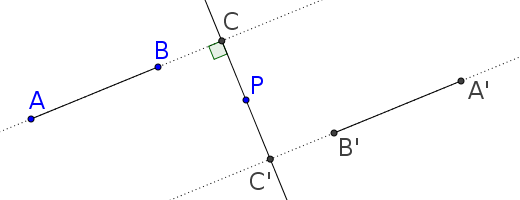
Dans le cas où P n’est pas aligné avec A et B, pour expliquer que [AB] et [A’B’] sont parallèles, une méthode consiste à rajouter un élément supplémentaire : l’angle droit ${ \widehat {\mbox{ACP}}}$ avec le point C sur la droite (AB) ; voyez la figure ci-dessous.

Le symétrique de ${ \widehat {\mbox{ACP}}}$ est l’angle ${ \widehat {\mbox{A’C’P}}}$ ; ils ont donc la même ouverture et donc ${ \widehat {\mbox{A’C’P}}}$ est aussi un angle droit.

Et comme C, P et C’ sont alignés on a donc les droites (AB) et (A’B’) qui sont toutes les deux perpendiculaires à la droite (CC’).

Or, 2 droites perpendiculaires à une même troisième droite sont parallèles, donc (AB) et (A’B’) sont parallèles. Ce qu’il fallait expliquer.

Retenez la méthode utilisée : avoir l’idée de rajouter un élément pour expliquer une propriété. C’est cette méthode qui est par exemple mise en œuvre pour résoudre des énigmes comme celle des 41 chameaux (voir la rubrique énigme).