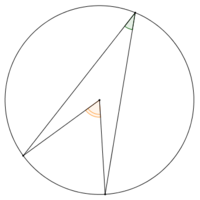
Théorème de l’angle inscrit
Théorème
Dans tout cercle, tout angle inscrit est égal à la moitié de l’angle au centre qui intercepte le même arc que l’angle inscrit.
Démonstration
Pour démontrer ce théorème, nous allons considérer trois cas, selon la position du centre du cercle par rapport aux côtés de l’angle inscrit :
- 1er cas : le centre est situé sur un des côtés de l’angle inscrit.
- 2e cas : le centre est situé entre les deux côtés de l’angle inscrit.
- 3e cas : le centre n’est pas situé entre les deux côtés de l’angle inscrit.
1er cas
Le centre est situé sur un des côtés de l’angle inscrit. Voici une figure qui correspond à ce cas :

$O$ est sur le segment $[SB]$
donc $\widehat{SOA}$ et $\widehat{AOB}$ sont supplémentaires.
Par ailleurs, dans le triangle $OSA$, $\widehat{SOA}$ est aussi supplémentaire avec la somme $\widehat{OSA} + \widehat{OAS}$ car la somme des trois angles d’un triangle est un angle plat,
donc $\widehat{AOB}$ = $\widehat{OSA} + \widehat{OAS}$.
Or, $OSA$ est isocèle en $O$ car $S$ et $A$ sont sur le cercle de centre $O$,
donc $\widehat{OSA}$ = $\widehat{OAS}$
donc $\widehat{AOB}$ = 2à—$\widehat{OSA}$
donc $\widehat{OSA}$ = $\frac{1}{2}\widehat{AOB}$ ce qui donne $\widehat{BSA}$ = $\frac{1}{2}\widehat{AOB}$ CQFD
2e cas
Le centre est situé entre les deux côtés de l’angle inscrit. Voici une figure qui correspond à ce cas :

L’idée principale est de rajouter le point qui est diamétralement opposé au sommet de l’angle inscrit pour faire apparaître des angles inscrits qui sont dans la situation du 1er cas :

On a donc $\widehat{ASB}$ = $\widehat{AST} + \widehat{BST}$ et $\widehat{AOB}$ = $\widehat{AOT} + \widehat{TOB}$
où $\widehat{AST}$ et $\widehat{BST}$ sont des angles inscrits qui correspondent au 1er cas.
Or, d’après le 1er cas, $\widehat{AST}$ = $\frac{1}{2}\widehat{AOT}$ et $\widehat{BST}$ = $\frac{1}{2}\widehat{TOB}$
donc $\widehat{ASB}$ = $\frac{1}{2}\widehat{AOT} + \frac{1}{2}\widehat{TOB}$ = $\frac{1}{2}(\widehat{AOT} + \widehat{TOB})$ = $\frac{1}{2}\widehat{AOB}$ CQFD
3e cas
Le centre n’est pas situé entre les deux côtés de l’angle inscrit. Voici une figure qui correspond à ce cas :

Comme pour le cas précédent, nous rajoutons le point qui est diamétralement opposé au sommet de l’angle inscrit :

On a donc $\widehat{ASB}$ = $\widehat{AST} - \widehat{BST}$ et $\widehat{AOB}$ = $\widehat{AOT} - \widehat{BOT}$
où $\widehat{AST}$ et $\widehat{BST}$ sont des angles inscrits qui correspondent au 1er cas.
Or, d’après le 1er cas, $\widehat{AST}$ = $\frac{1}{2}\widehat{AOT}$ et $\widehat{BST}$ = $\frac{1}{2}\widehat{BOT}$
donc $\widehat{ASB}$ = $\frac{1}{2}\widehat{AOT} - \frac{1}{2}\widehat{BOT}$ = $\frac{1}{2}(\widehat{AOT} - \widehat{BOT})$ = $\frac{1}{2}\widehat{AOB}$ CQFD
Cas particulier
Un cas particulier important est le cas où l’angle au centre est un angle plat :
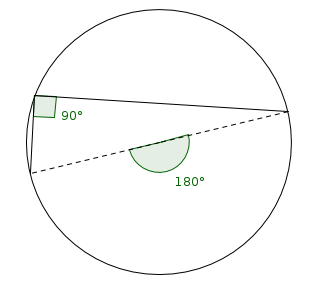
On retrouve alors le théorème du triangle inscrit dans un demi-cercle :
Dans tout cercle, si un triangle a ses trois sommets sur le cercle et si un côté est un diamètre alors ce triangle est un triangle rectangle.
