Théorème

Si un triangle $ABC$ est isocèle en $A$ alors les angles $\widehat{ABC}$ et $\widehat{ACB}$ sont égaux.

Démonstration

Considérons un triangle $ABC$ est isocèle en $A$ :

$ABC$ est isocèle en $A$ donc $AB=AC$

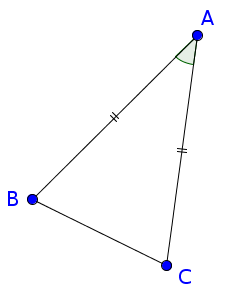
On a $\widehat{BAC}=\widehat{CAB}$ avec $AB=AC$ : on peut donc retourner le triangle sur lui-même de sorte que B se superpose en et, C se superpose en B, le sommet $A$ restant sur lui-même.

Il en résulte que les angles $\widehat{ABC}$ et $\widehat{ACB}$ se superposent et donc sont égaux. CQFD