Théorème

Le volume d’un prisme est égal au produit de sa hauteur par l’aire de sa base.

Quelques précisions

Une grande partie de la démonstration ne concerne que les prismes droits car les prismes obliques ne sont pas au programme du collège ; vous trouverez cependant une indication succincte concernant les prismes obliques pour lesquels la règle de calcul est encore valable, la hauteur étant la distance entre les deux bases parallèles.

La démonstration de la règle de calcul du volume présentée ici est basée sur un découpage de la base en triangles, ce qui donne un découpage du prisme en prismes à bases triangulaires, prismes ayant tous la même hauteur. On montre pourquoi la règle est vraie dans le cas d’une base triangulaire, ce qui permet de l’obtenir pour le cas d’une base polygonale quelconque.

D’ailleurs, en pratique, pour calculer l’aire de la base formée par un polygone qui n’est pas un parallélogramme, on partage le polygone en triangles : on calcule les aires de ces triangles puis on additionne les résultats pour obtenir l’aire du polygone.

Démonstration

– Cas d’un prisme droit à base triangulaire rectangle
Dans ce cas, la base est la moitié d’un rectangle donc le prisme est la moitié du pavé droit dont la base est ce rectangle et la hauteur celle du prisme. Voici une figure qui montre cette situation :

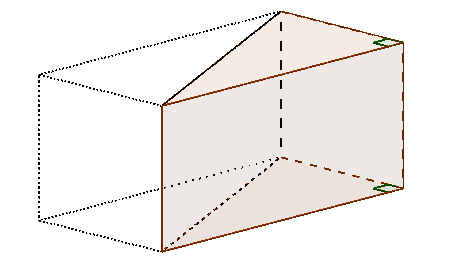
Ainsi, le volume du prisme est la moitié du volume du pavé droit.

Or le volume du pavé droit est le produit de sa hauteur par l’aire du rectangle qui constitue sa base, et ce rectangle est le double du triangle qui constitue la base du prisme.

Il en résulte que le volume du prisme est le produit de sa hauteur par l’aire de sa base.

– Cas d’un prisme droit à base triangulaire
Dans ce cas, on peut toujours partager la base en deux triangles rectangles et donc partager le prisme en deux prismes à bases triangulaires rectangles, chaque prisme ayant la même hauteur, comme sur la figure suivante :

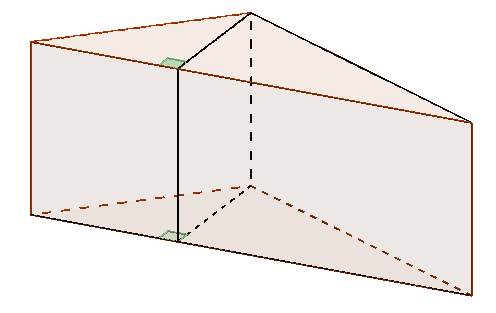
Le volume du prisme est la somme des volumes des deux prismes dont les bases sont des triangles rectangles. Pour chacun de ces deux prismes, le volume est égal au produit de sa hauteur par l’aire de sa base. La somme de ces deux produits, qui ont le même facteur avec la hauteur commune aux différents prismes, peut donc être mis sous la forme du produit de cette hauteur par la somme des aires des deux triangles rectangles. Et comme cette somme est égale à l’aire de la base du prisme, il en résulte encore que le volume du prisme est le produit de sa hauteur par l’aire de sa base.

– Cas d’un prime droit à base polygonale
Pour fixer les idées, supposons que la base soit un pentagone (Le raisonnement est le même quelque soit le nombre de côtés du polygone). Soit par exemple la figure suivante :

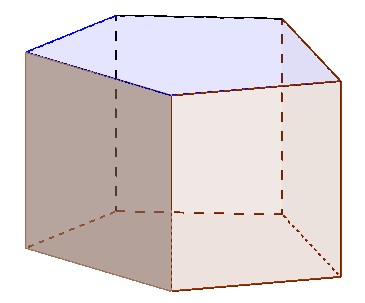
Partageons la base pentagonale en trois triangles : on obtient alors un partage du prisme en trois prismes droits dont les bases sont des triangles et dont les hauteurs sont égales à celle du prisme.

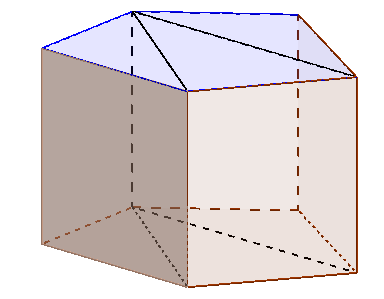
Le volume du prisme est égal à la somme des volumes des trois prismes à bases triangulaires. Or, chacun de ces prismes a un volume obtenu en multipliant l’aire de sa base par la hauteur du prisme, cette hauteur étant la même pour les trois prismes. La somme des trois produits est donc le produit de la hauteur par la somme des aires des trois triangles qui composent la base pentagonale : ce qui donne le produit de la hauteur par l’aire de la base. Ainsi, le volume du prisme est égal au produit de sa hauteur par l’aire de sa base.

– cas d’un prisme oblique
Si on a un prisme oblique, on peut le découper à l’aide d’une section perpendiculaire aux faces du prisme, comme le montre la figure suivante :

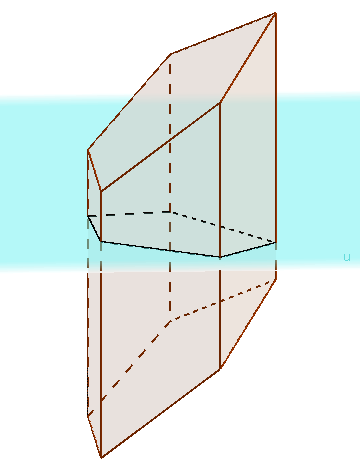
Ce découpage permet d’obtenir deux morceaux que l’on peut alors déplacer (en plaçant le morceau qui est en dessous au dessus de l’autre) pour obtenir un prisme droit. Le volume est alors obtenu par le produit de la longueur d’une arête latérale par l’aire de la section perpendiculaire.

Pour montrer que la formule obtenue pour les prismes droits est encore valable pour les prismes obliques, on pourra reprendre les différents cas en considérant d’abord un prisme à base triangulaire et le compléter pour obtenir un pavé oblique dont le volume est équivalent au volume d’un pavé droit de même hauteur et de base équivalente. Cette partie est donc hors programme et ne sera pas détaillée.