Vous trouverez ci-dessous des démonstrations des trois propriétés liées aux milieux des côtés d’un triangle.

Ces propriétés sont liées au théorème de Thalès comme cela est montré dans l’article consacré à ce théorème. Par ailleurs, on peut démontrer le théorème de Thalès à partir du théorème de la droite des milieux.

Le théorème de la droite des milieux

Pour tout triangle, la droite qui passe par les milieux de deux côtés est parallèle au troisième côté.

 

Démonstration :

– Soit un triangle $ABC$ avec $D$ le milieu du côté $[AB]$ et $E$ le milieu de $[AC]$. Il s’agit d’expliquer pourquoi les droites $(DE)$ et $(BC)$ sont parallèles.

Soit $H$ le point d’intersection de la hauteur issue de $A$ avec la droite $(BC)$ : les triangles $ACH$ et $ABH$ sont rectangles en $H$.

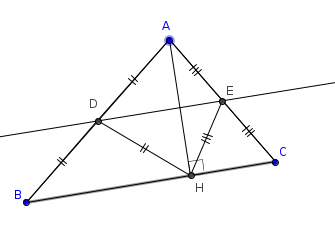
Comme $E$ est le milieu du côté $[AC]$, $E$ est le centre du cercle circonscrit au triangle rectangle $ACH$
donc $AE = EH$
donc $E$ est sur la médiatrice de $[AH]$.

De même, comme $D$ est le milieu de $[AB]$, $D$ est le centre du cercle circonscrit au triangle rectangle $ABH$
donc $AD = DH$
donc $D$ est sur la médiatrice de $[AH]$.

Ainsi, $(DE)$ est la médiatrice de $[AH]$
donc $(DE)$ est perpendiculaire à $(AH)$
Or, $(BC)$ est aussi perpendiculaire à $(AH)$
donc les droites $(DE)$ et $(BC)$ sont parallèles.

 

Le théorème de la parallèle et du milieu

Pour tout triangle, la droite parallèle à un côté passant par le milieu d’un deuxième côté passe par le milieu du troisième côté.

 

Démonstration :

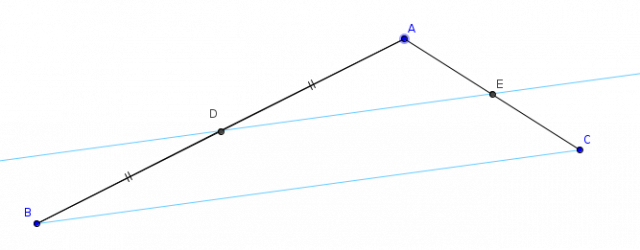
– Soit un triangle $ABC$ avec $D$ le milieu du côté $[AB]$ et $E$ le point d’intersection de la parallèle au côté $[BC]$ passant par $D$. Il s’agit d’expliquer pourquoi $E$ est le milieu de $[AC]$.

Considérons $K$ est le symétrique de $E$ par rapport à $D$ : le point $D$ est le milieu de $[KE]$.

Ainsi, $D$ est le milieu de $[AB]$ et de $[KE]$ donc $AKBE$ est un parallélogramme
donc $(KB)$ et $(AC)$ sont parallèles
Or, $(KE)$ et $(BC)$ sont parallèles donc $KECB$ est un parallélogramme.

$AKBE$ est un parallélogramme donc $KB = AE$
$KECB$ est un parallélogramme donc $KB = EC$
donc $AE = EC$
comme $A$, $E$ et $C$ sont alignés, cela nous montre que $E$ est le milieu de $[AC]$.

 

Le segment des milieux

Pour tout triangle, le segment qui joint les milieux de deux côtés est égal à la moitié du troisième côté.

 

Démonstration :

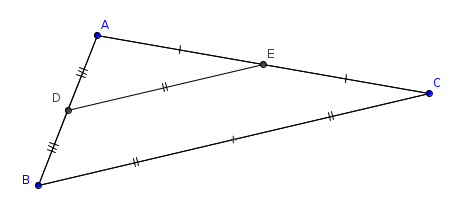
– Soit $ABC$ un triangle avec $D$ le milieu de $[AB]$ et $E$ le milieu de $[AC]$. Il s’agit d’expliquer que $DE$ est la moitié de $BC$.

Pour cela, appelons $F$ le milieu de $[BC]$.
Dans le triangle $ABC$, $D$ est le milieu de $[AB]$ et $E$ est le milieu de $[AC]$
donc $(DE)$ // $(BC)$
Dans le triangle $ABC$, $F$ est le milieu de $[BC]$ et $E$ est le milieu de $[AC]$
donc $(FE)$ // $(AB)$
Ce qui0 montre que $DEFB$ est un parallélogramme
donc $DE = BF$
Or, $BF$ est la moitié de $BC$
donc $DE$ est la moitié de $BC$.

Remarque : regardez bien la figure obtenue dans la démonstration : le triangle $ABC$ se trouve partagé en 4 triangles identiques. Ainsi, le triangle $ADE$ a ses côtés qui mesurent la moitié des côtés du triangle $ABC$ mais l’aire du triangle $ADE$ est égal au quart de l’aire du triangle $ABC$.

 

Le théorème de Varignon

Pour tout quadrilatère, les milieux de ses côtés sont les sommets d’un parallélogramme.

La démonstration de ce théorème utilise plusieurs fois le théorème de la droite des milieux dans des triangles que je vous laisse trouver…